Cross Validation
Introduction
Here we overview two approaches to overcome some of the challenges associated with train, valid and test splits.
LOOCV (Leave-One-Out Cross Validation)
In LOOCV, a single observation is left out for the validation set. This leaves the remaining observations for train and/or test. We train the model like usual, and use the single validation observation as the test for that data point.
Then, we repeat that process across each individual observation, starting with ($x_1$,$y_1$), then ($x_2$,$y_2$), etc. Then, after getting the MSE (Mean Squared Error) for each LOOCV, take the average of these validation error estimates:
$ CV_n = \frac{1}{n}\sum_{i=1}^{n}MSE_i $
Where n is the number of observations.
Here’s a simple example of running through each validation set. Sometimes, the test split is called the validation split (meaning they only split the data into 2 splits, not 3), as you see in the animation below.
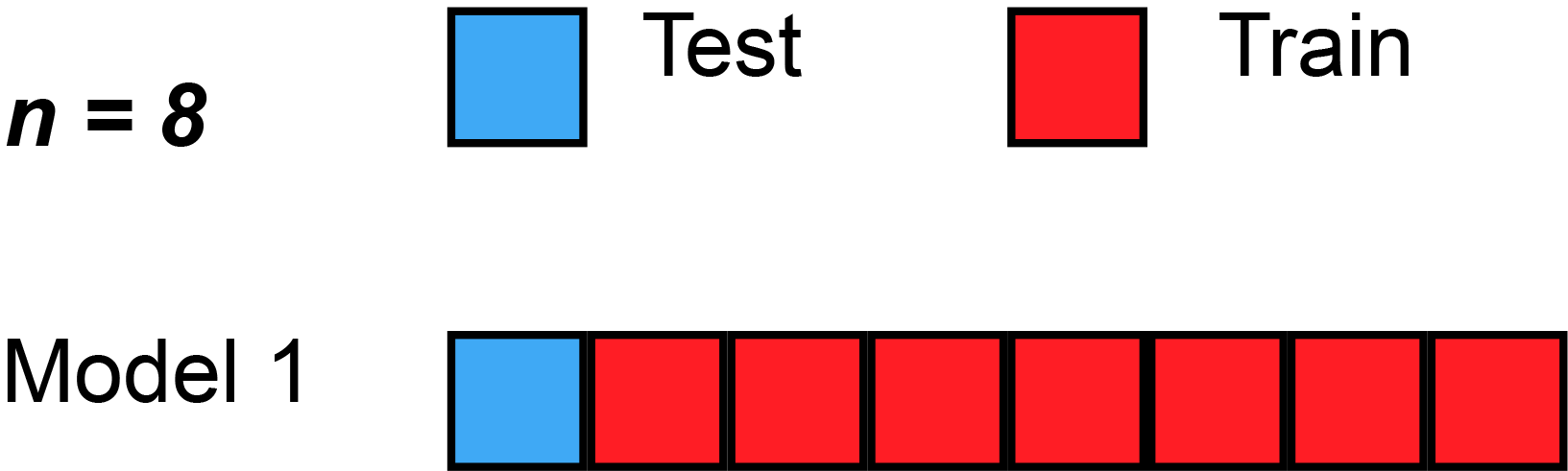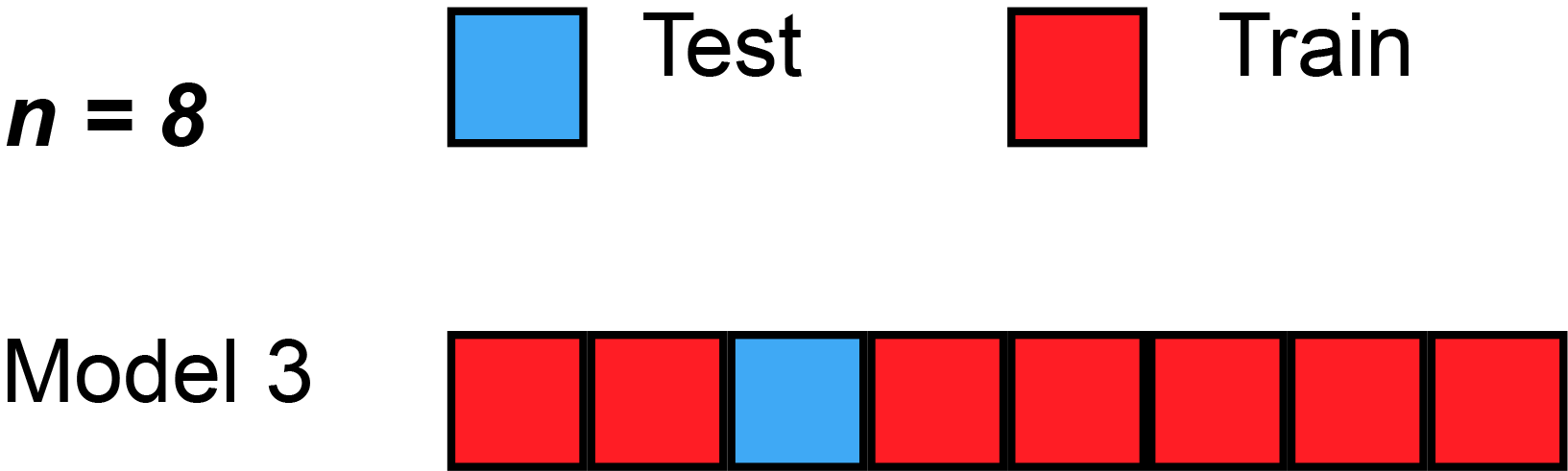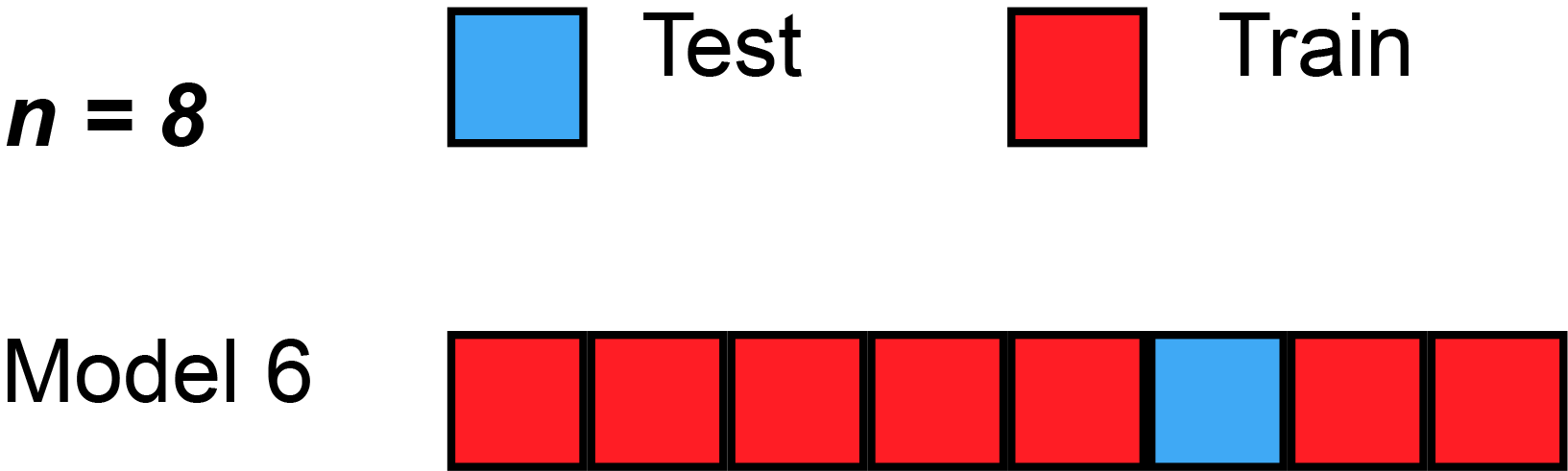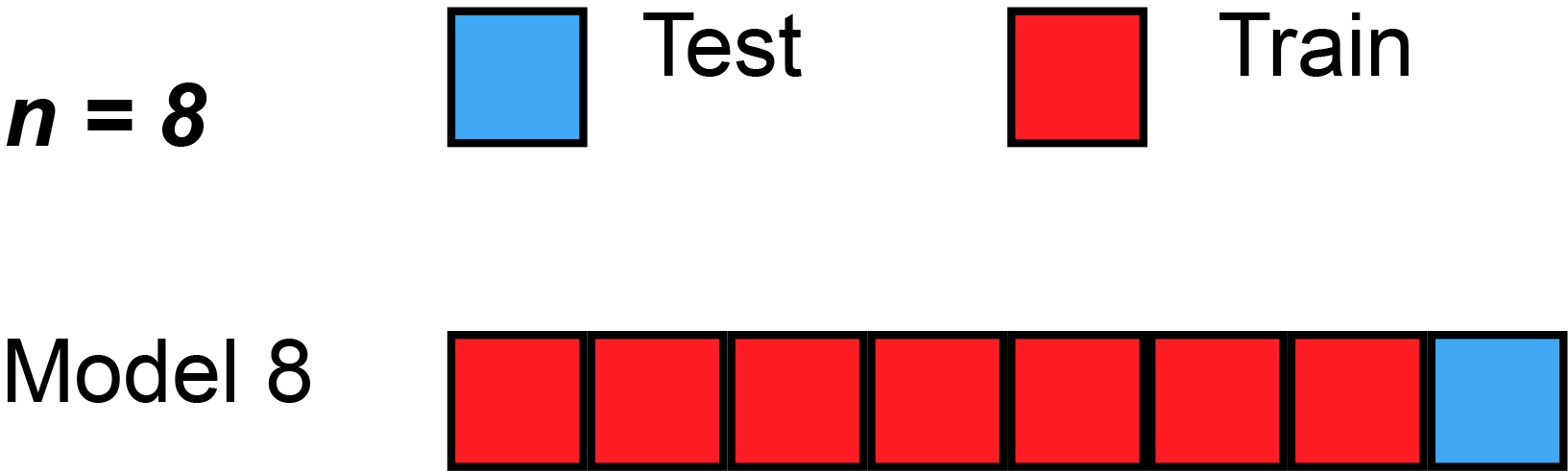
Strengths With LOOCV
-
Far less bias (see Bias-Variance Tradeoff) because the validation error rate is often not overestimated granted that far more of the data set is used for training in LOOCV
-
There is no randomness in the results, since each observation is used for validation exactly once
-
Very general and easy to implement with just about any predictive modeling
K-fold Cross Validation
K-fold CV is similar to LOOCV, except instead of 1 observation per validation split, we split the data into k number of "folds", or groups of approximately equal size. See the animation below for a visual explanation.
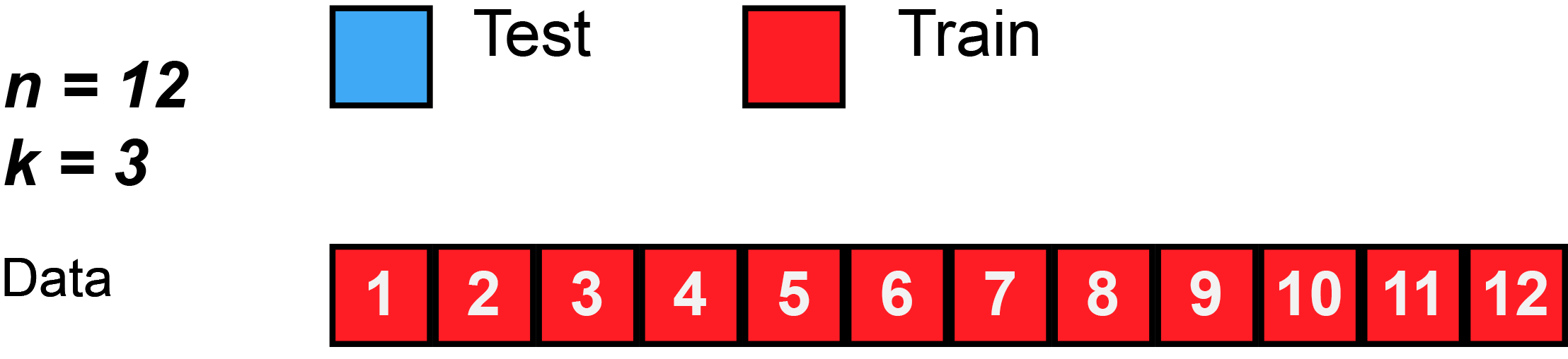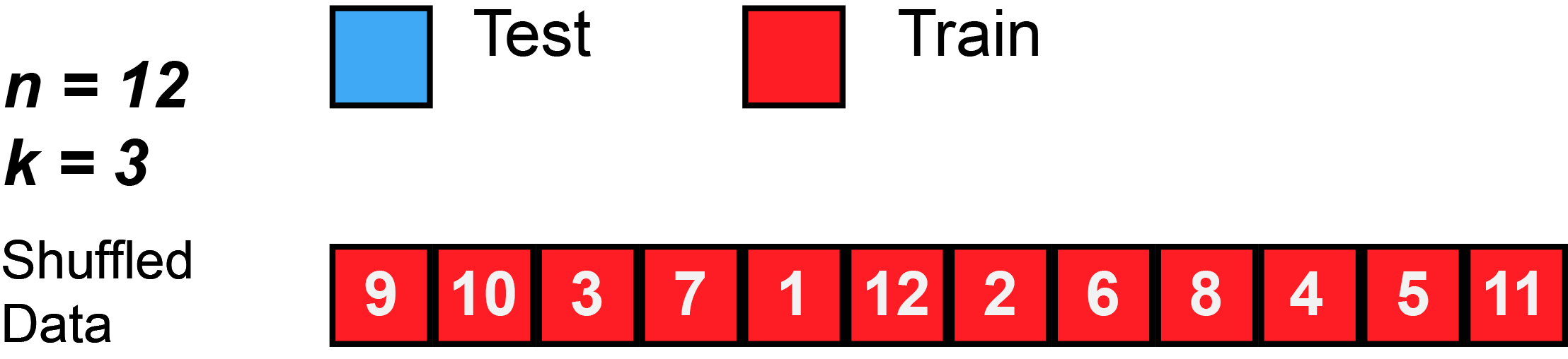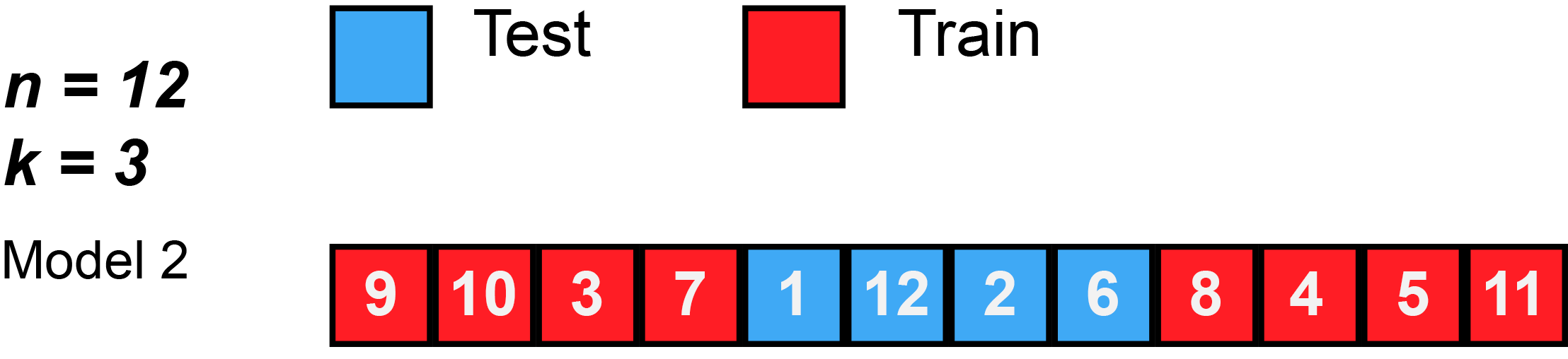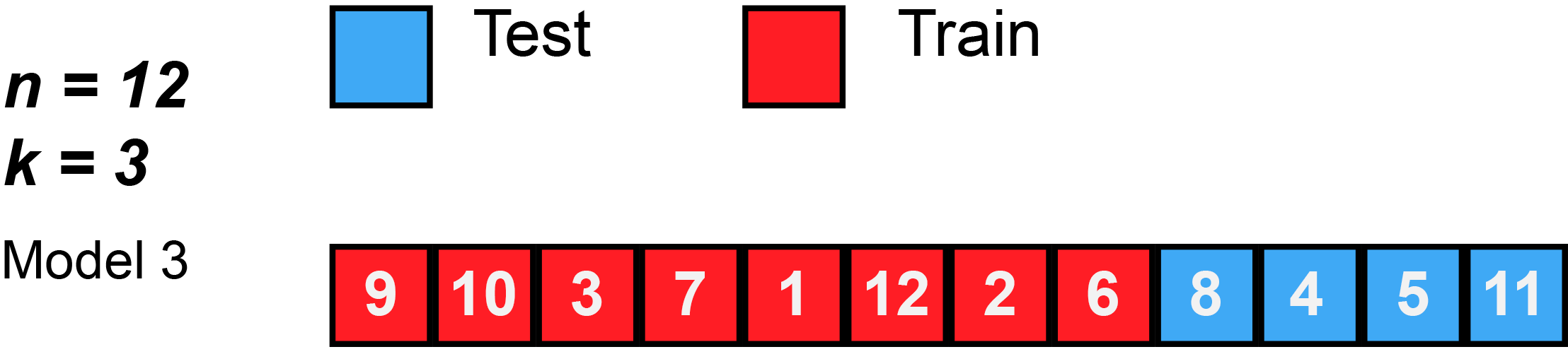
Again, this animation uses test to mean the validation split, because there isn’t a separate test split. First, k number of folds are chosen. In this animation, $k=3$. Then, the data is randomly shuffled. Then, each fold is given 4 observations, since 12 observations divided by 3 folds equals 4 observations per fold (sometimes you will have unequal folds; that’s OK, just try to make them as equal as possible).
This is how you compute the MSE mathematically using k-fold CV:
$ CV_k = \frac{1}{k}\sum_{i=1}^{k}MSE_k $
The Right k
How can we choose the right size of k? One of the strengths of k-folding is that it requires less computation than LOOCV, but as k increases, this becomes less and less the case. At the extreme, when k=n, that would be the same as LOOCV. On the other extreme, if k=2, then you are only taking 2 average MSE’s.
The rule of thumb is typically a lower number is preferred, usually around 5-10. But instead of trying just one number, just try many k values and see which gives the best accuracy, or whatever metric you want to measure by! Let the data drive your k decision. Often there is an approximately optimal k value, but it is highly contextual and depends on the problem.
Strengths With k-fold
If you recall from LOOCV, one of the challenges is that it has to be computed n times. And as you get more and more data, this can be computationally expensive. K-folds simplify this computation: you end up doing precisely k computations, compared to n computations in LOOCV.
Another advantage of k-folds is that they introduce an element of Bias-Variance Tradeoff. The details for this are outside of the scope of this article, but in general, an increasingly high k value will lead to higher variance, and vice versa. Again, there are empirical studies which show that k=5 to k=10 is usually the approximately optimal value of k. But why trust these empirical studies? See for yourself which k is best for your data!